Sheet 3

Exercise 1 (Convergence Speed).

Proof that

1. if we have

   $$\underset{k\to \mathrm{\infty }}{lim\; sup}\frac{e(x_{k+1})}{e(x_k)}=0,$$

   then $e(x_k)$ converges super-linearly.

   Solution.

   We define $c_n:={sup}_{k\ge n}\frac{e(x_{k+1})}{e(x_k)}$. Then

   $$\underset{n\to \mathrm{\infty }}{lim}{c}_n=\underset{k\to \mathrm{\infty }}{lim\; sup}\frac{e(x_{k+1})}{e(x_k)}=0$$

   and by definition

   $$e(x_{k+1})\le c_{k}e(x_k).$$

   Thus we have super-linear convergence. ∎

2. If for $c\in (0,1)$ we have

   then $e(x_k)$ converges linearly with rate $c$.

   Solution.

   We again define $c_n:={sup}_{k\ge n}\frac{e(x_{k+1})}{e(x_k)}$

   thus there exists $N\ge 0$ such that for all $n\ge N$ we have $c_n\le c$ and therefore for all $n\ge N$

   $$e(x_{n+1})\le c_{n}e(x_n)\le ce(x_n).\mathit{∎}$$

3. If for $c\in (0,1)$ we have

   then $e(x_k)$ converges super-linearly with rate $c$.

   Solution.

   We similarly define $c_n:={sup}_{k\ge n}\frac{e(x_{k+1})}{e{(x_k)}^2}$ and again get . Thus there exists $N\ge 0$ such that for all $n\ge K$ we have $c_n\le c$ and therefore for all $n\ge N$

   $$e(x_{n+1})\le c_{n}e{(x_n)}^2\le ce{(x_n)}^2.\mathit{∎}$$

Exercise 2 (Sub-gradients).

Let $f\mathrm{,}g\mathrm{:}{ℝ}^d\mathrm{\to }ℝ$ be convex functions.

1. Prove that $\partial f(x)$ is a convex set for any $x\in {ℝ}^d$.

   Solution.

   Let $g_1,g_2\in \partial f(x)$. Then for any $\lambda \in [0,1]$ and any $y\in {ℝ}^d$

   $f(y)$ $=\lambda f(y)+(1-\lambda )f(y)$

   ≥λ(f(x) + ⟨g_1, y-x⟩) + (1-λ) (f(x) + ⟨g_2, y-x⟩)

   $=f(x)+⟨\lambda g_1+(1-\lambda )g_2,y-x⟩$

   thus $\lambda g_1+(1-\lambda )g_2\in \partial f(x)$ by definition. ∎

2. Prove for $a>0$, $\partial (af)=a\partial f$

   Solution.

   We only need to prove “$\supseteq$”. Using $\tilde{f}=af$ with $\tilde{a}=\frac{1}{a}$ the other inclusion immediately follows.

   Let $a{g}_x\in a\partial f(x)$ with $g_x\in \partial f(x)$. We need to show that $a{g}_x\in \partial (af)(x)$. But this follows immediately

   $$\underset{>0}{\underbrace{a}}f(y)\stackrel{g_x\in \partial f(x)}{\ge }a\left(f(x)+⟨g_x,y-x⟩\right)=(af)(x)+⟨a{g}_x,y-x⟩.\mathit{∎}$$

3. Prove that $\partial (f_1+f_2)\supseteq \partial f_1+\partial f_2$

   Solution.

   Let $g_i\in \partial f_i(x)$ for $i=1,2$. Then we have that $g_1+g_2\in \partial (f_1+f_2)$ because

   $(f_1+f_2)(y)$ $\ge \left(f_1(x)+⟨g_1,y-x⟩\right)+\left(f_2(x)+⟨g_2,y-x⟩\right)$

   $=(f_1+f_2)(x)+⟨g_1+g_2,y-x⟩.\mathit{∎}$

4. For $h(x)=f(Ax+b)$ prove $\partial h(x)\supseteq A^T\partial f(Ax+b)$. Prove equality for invertible $A$.

   Solution.

   Let $g_x\in \partial f(x)$ i.e. $g_{Ax+b}\in \partial f(Ax+b)$. Then $A^T{g}_{Ax+b}\in \partial h(x)$ because

   $h(y)=f(Ay+b)$ $\ge f(Ax+b)+⟨g_{Ax+b},(Ay+b)-(Ax+b)⟩$

   $=h(x)+⟨A^T{g}_{Ax+b},y-x⟩.$

   If $A$ is invertible, we have $f(x)=h(A^{-1}x-A^{-1}b)$ so by the previous statement with $\tilde{A}=A^{-1}$ and $\tilde{b}=-A^{-1}b$, we get the other direction. ∎

   Exercise 3 (Lasso).

   Let

   $$f(x)=\frac{1}{2}{\parallel x-y\parallel }^2+\lambda {\parallel x\parallel }_1$$

   for $x\mathrm{\in }{ℝ}^d$ be the Lagrangian form of the least squares LASSO method.

   1. Compute a sub-gradient of $f$.

      Solution.

      Using $\partial (g+\lambda h)(x)\supseteq \partial g(x)+\lambda \partial h(x)$, we only need to determine the subgradient of $g(x):=\frac{1}{2}{\parallel x-y\parallel }^2$ and

      $$h(x):={\parallel x\parallel }_1=\sum _{i=1}^d|x_i|.$$

      But $\nabla g(x)=x-y$ as $g$ is differentiable. And since it is also convex, we have

      $$\partial g(x)=\{\nabla g(x)\}.$$

      Now the subgradient of $h_i(x)=|x_i|$ is given by $sgn(x_i)e_i$, where $sgn(0)\in [-1,1]$ can be selected arbitrarily, because

      $h_i(x)+⟨sgn(x_i)e_i,y-x⟩$ $=|x_i|+sgn(x_i)y_i-\underset{|x_i|}{\underbrace{sgn(x_i)x_i}}=sgn(x_i)y_i$

      So again

      $$\partial h(x)\supseteq \sum _{i=1}^d\partial h_i(x)\ni {(sgn(x_1),\mathrm{\dots },sgn(x_n))}^T=:s(x).$$

      So putting everything together we have

      $$\partial f(x)\ni x-y+\lambda s(x).\mathit{∎}$$

   2. Prove that $f$ is convex.

      Solution.

      As its sets of sub-gradients is nowhere empty, it is convex. ∎

   3. Find a global minimum of $f$.

      Solution.

      By the lecture it is sufficient to find a point $x$ such that $0\in \partial f(x)$. By the previous exercise we therefore want to solve

      $$0\stackrel{!}{=}x-y+\lambda s(x)$$

      entry-wise this implies

      $x_i$= y_i - λsgn(x_i) = { y i + λ x i ¡ 0 y i - λ[-1, 1] x i = 0 y i - λ x i ¿ 0

   4. Implement $f$ as a sub-type of ”DifferentiableFunction” (even though it is not) by returning a single sub-gradient and apply gradient descent to verify the global minimum https://classroom.github.com/a/XqNuifmO .

      Exercise 4 (Momentum Matrix).

      let $D\mathrm{=}\mathrm{diag}\mathit{}\mathrm{(}{\lambda }_{\mathrm{1}}\mathrm{,}\mathrm{\dots }\mathrm{,}{\lambda }_d\mathrm{)}$, $\alpha \mathrm{,}\beta \mathrm{>}\mathrm{0}$ and define

      Prove there exists a regular $S\mathrm{\in }{ℝ}^{\mathrm{2}\mathit{}d\mathrm{\times }\mathrm{2}\mathit{}d}$ such that

      with

      Solution.

      We simply define for the standard basis $e_i\in {ℝ}^d$

      in particular $S^T=S^{-1}$. ∎

      Exercise 5 (PL-Inequality).

      Assume $f\mathrm{:}{ℝ}^d\mathrm{\to }ℝ$ is $L$-smooth and satisfies the Polyak-Łojasiewicz inequality

      $${\parallel \nabla f(x)\parallel }^2\ge 2c(f(x)-f_{*})$$ (PL)

      for some $c\mathrm{>}\mathrm{0}$ and all $x\mathrm{\in }{ℝ}^d$ with $f_{\mathrm{*}}\mathrm{=}{\min }_x\mathit{}f\mathit{}\mathrm{(}x\mathrm{)}\mathrm{>}\mathrm{-}\mathrm{\infty }$.

      1. Prove that gradient descent with fixed step size ${\alpha }_k=\frac{1}{L}$ converges linearly in the sense

         $$f(x_k)-f_{*}\le {(1-\frac{c}{L})}^k(f(x_0)-f_{*}).$$

         Solution.

         By $L$-smoothness and the descent lemma, we have

         $$f(x_{k+1})\le f(x_k)-\frac{1}{2L}{\parallel \nabla f(x_k)\parallel }^2\stackrel{(\text{<a href="\#S0.Ex32" title="(PL) ‣ Exercise 5 (PL-Inequality). ‣ item (iv)(d) ‣ Exercise 3 (Lasso). ‣ item (iv) ‣ Exercise 2 (Sub-gradients). ‣ Sheet 3" class="ltx\_ref ltx\_font\_italic"><span class="ltx\_text ltx\_ref\_tag">PL</span></a>})}{\le }f(x_k)-\frac{c}{L}(f(x_k)-f_{*}).$$

         Subtracting $f_{*}$ from both sides, we get

         $$f(x_{k+1})-f_{*}\le (1-\frac{c}{L})(f(x_k)-f_{*})\mathit{∎}$$

      2. Prove that $\mu$-strong-convexity and $L$-smoothness imply the PL-inequality.

         Solution.

         Recall by the solution of sheet 1, exercise 6 (iii), and strong convexity we have

         $\mu {\parallel x-y\parallel }^2$ $\le D_f^{(B)}(x,y)+D_f^{(B)}(y,x)$

         $=⟨\nabla f(x)-\nabla f(y),x-y⟩$

         and therefore

         $$\mu \parallel x-y\parallel \le \parallel \nabla f(x)-\nabla f(y)\parallel .$$ (1)

         Finally we know by $L$-smoothness and $\nabla f(x_{*})=0$ where $x_{*}$ is the minimum

         $$f(x)-f(x_{*})\stackrel{\nabla f(x_{*})=0}{=}{D}_f^{(B)}(x,x_{*})\stackrel{L\text{-smooth}}{\le }\frac{L}{2}{\parallel x-x_{*}\parallel }^2\stackrel{(\mathit{\text{<a href="\#S0.E1" title="(1) ‣ item (iv)((d))(II) ‣ Exercise 5 (PL-Inequality). ‣ item (iv)(d) ‣ Exercise 3 (Lasso). ‣ item (iv) ‣ Exercise 2 (Sub-gradients). ‣ Sheet 3" class="ltx\_ref ltx\_font\_italic"><span class="ltx\_text ltx\_ref\_tag">1</span></a>}})}{\le }\frac{L}{2\mu }{\parallel \nabla f(x)-\underset{=0}{\underbrace{\nabla f(x_{*})}}\parallel }^2.\mathit{∎}$$

      3. Use a graphing calculator to find $c$ such that $f(x)=x^2+3{\sin }^2(x)$ satisfies the PL-condition (argue why $x\to \mathrm{\infty }$ is not a problem) and prove it is not convex.

         Solution.

         For $c=\frac{1}{6}$ we have the PL-condition

         

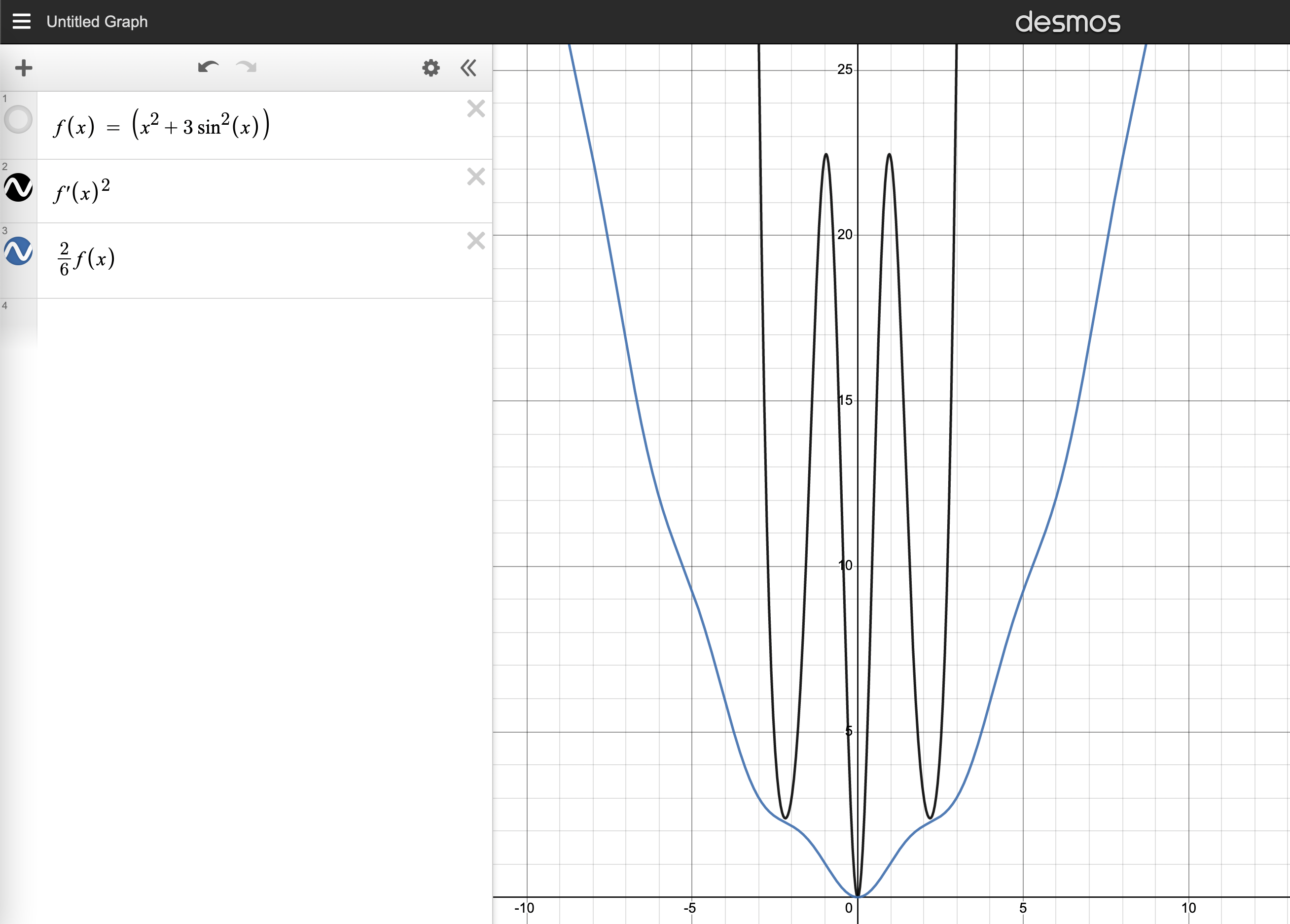
         As $f^{\prime }(x)=2(x+3\sin (x)\cos (x))$ and therefore

         $$f^{\prime }{(x)}^2=4{(x+3\underset{\in [-1,1]}{\underbrace{\sin (x)\cos (x)}})}^2\stackrel{|x|\ge 3}{\ge }4{(|x|-3)}^2$$

         the $x^2$ dominates for large $x$, so if we make $c$ small enough we can ensure the inequality for large $x$.

         $f$ is not convex because

         $$f(\frac{1}{2}\pi +\frac{1}{2}0)=\frac{{\pi }^2}{4}+3>\frac{1}{2}{\pi }^2=\frac{1}{2}f(\pi )+\frac{1}{2}f(0).$$

         ∎

         Exercise 6 (Weak PL-Inequality).

         Assume $f\mathrm{:}{ℝ}^d\mathrm{\to }ℝ$ is $L$-smooth and satisfies the “weak PL inequality”

         $$\parallel \nabla f(x)\parallel \ge 2c(f(x)-f_{*})$$

         for some $c\mathrm{>}\mathrm{0}$ and all $x\mathrm{\in }{ℝ}^d$ with $f_{\mathrm{*}}\mathrm{=}{\min }_x\mathit{}f\mathit{}\mathrm{(}x\mathrm{)}\mathrm{>}\mathrm{-}\mathrm{\infty }$.

         1. Let $a_0\in [0,\frac{1}{q}]$ for some $q>0$ and assume for the sequence ${(a_n)}_{n\in \mathbb{N}}$ that it is positive and satisfies a diminishing contraction

            $$0\le a_{n+1}\le (1-q{a}_n)a_n\mathit{\hspace{1em}\hspace{1em}}\forall n\ge 0.$$

            Prove the convergence rate

            $$a_n\le \frac{1}{nq+1/a_0}\le \frac{1}{(n+1)q}.$$

            Hint.

            A useful checkpoint might be the telescoping sum of

            $$\frac{1}{a_{n+1}}-\frac{1}{a_n}\ge q.$$

            Solution.

            Divide the reordered contraction

            $$a_n\ge a_{n+1}+q{a}_n^2$$

            by $a_n{a}_{n+1}$ to obtain

            $$\frac{1}{a_{n+1}}\ge \frac{1}{a_n}+q\underset{\ge 1}{\underbrace{\frac{a_n}{a_{n+1}}}}\ge \frac{1}{a_n}+q$$

            which leads to

            $$\frac{1}{a_n}-\frac{1}{a_0}=\sum _{k=0}^{n-1}\frac{1}{a_{k+1}}-\frac{1}{a_k}\ge nq.$$

            Reordering we obtain our claim

            $$a_n\le \frac{1}{nq+\frac{1}{a_0}}\stackrel{a_0\le \frac{1}{q}}{\le }\frac{1}{(n+1)q}.\mathit{∎}$$

         2. Prove that $f$ is bounded. More specifically $e(x):=f(x)-f_{*}\le \frac{L}{2c^2}$ for all $x$.

            Hint.

            Use Sheet 1 Exercise 1 (i).

            Solution.

            Using Sheet 1 Exercise 1 (i), we get

            $$f_{*}\le f(x)-\frac{1}{2L}{\parallel \nabla f(x)\parallel }^2$$

            and therefore

            $$e(x)\ge \frac{1}{2L}{\parallel \nabla f(x)\parallel }^2\stackrel{\text{weak PL}}{\ge }\frac{4c^2}{2L}e{(x)}^2.$$

            Dividing both sides by $e(x)$ we obtain

            $$1\ge \frac{2c^2}{L}e(x)$$

            and thus

            $$e(x)\le \frac{L}{2c^2}.\mathit{∎}$$

         3. For gradient descent $x_{n+1}-x_n=-{\alpha }_n\nabla f(x_n)$ with constant step size ${\alpha }_k=\frac{1}{L}$ prove the convergence rate

            $$f(x_n)-f_{*}\le \frac{L}{2c^2(n+1)}.$$

            Solution.

            Using $L$-smoothness, we have

            $f(x_{k+1})$ $\le f(x_k)+⟨\nabla f(x_k),x_{k+1}-x_k⟩+\frac{L}{2}{\parallel x_{k+1}-x_k\parallel }^2$

            $\le f(x_k)-\underset{=\frac{1}{2L}}{\underbrace{{\alpha }_k(1-\frac{L}{2}{\alpha }_k)}}\underset{\ge 4c^{2}e{(x_k)}^2}{\underbrace{{\parallel \nabla f(x_k)\parallel }^2}}$

            If we subtract $f_{*}$ from both sides and apply our weak PL inequality we get

            $$e(x_{k+1})\le e(x_k)-\frac{4c^2}{2L}e{(x_k)}^2=(1-\frac{2c^2}{L}e(x_k))e(x_k)$$

            with $q=\frac{2c^2}{L}$ and $e(x_0)\le \frac{L}{2c^2}=\frac{1}{q}$ by (iv)(III)B, we can apply (iv)(III)A to obtain our claim. ∎